 LSM 树
LSM 树
使用场景:很多 NoSQL 数据库的底层存储引擎都是 LSM 树,如 RocksDB、LevelDB、HBase 以及 Prometheus 等。相比于B/B+树或者倒排索引,LSMTree采用了“疯狂到不顾一切”的干啥都磁盘顺序写的方案,赋予了它无与伦比的写吞吐量。
# 1. LSM 树数据结构定义
LSM 树并没有一种固定死的实现方式,更多的是一种将几种特性统一在一起的思想:
- “磁盘顺序写”
- “多个树(状数据结构)”
- “冷热(新老)数据分级”
- “定期归并”
- “非原地更新”
LSM树的定义:
- LSM树是一个横跨内存和磁盘的,包含多颗"子树"的一个森林。
- LSM树分为Level 0,Level 1,Level 2 ... Level n 多颗子树,其中只有Level 0在内存中,其余Level 1-n在磁盘中。
- 内存中的Level 0子树一般采用排序树(红黑树/AVL树)、跳表或者TreeMap等这类有序的数据结构,方便后续顺序写磁盘。
- 磁盘中的Level 1-n子树,本质是数据排好序后顺序写到磁盘上的文件,只是叫做树而已。
- 每一层的子树都有一个阈值大小,达到阈值后会进行合并,合并结果写入下一层。
- 只有内存中数据允许原地更新,磁盘上数据的变更只允许追加写,不做原地更新。
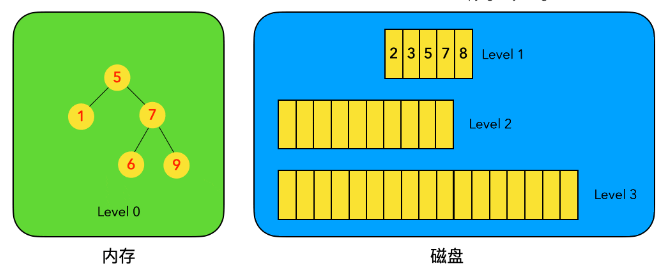
以上6条定义组成了LSM树,如下图。
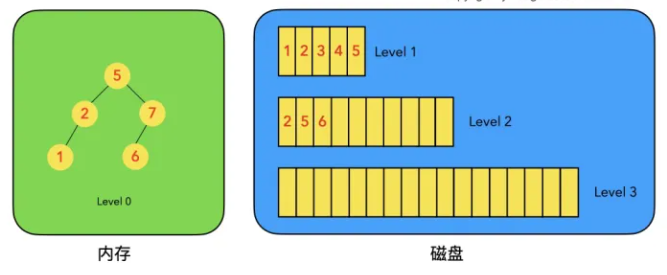
- 图1中分成了左侧绿色的内存部分和右侧蓝色的磁盘部分(定义1)。
- 图1左侧绿色的内存部分只包含Level 0树,右侧蓝色的磁盘部分则包含Level 1-n等多棵"树"(定义2)
- 图1左侧绿色的内存部分中Level 0是一颗二叉排序树(定义3)。注意这里的有序性,该性质决定了LSM树优异的读写性能。
- 图1右侧蓝色的磁盘部分所包含的Level 1到Level n多颗树,虽然叫做“树”,但本质是按数据key排好序后,顺序写在磁盘上的一个个文件(定义4) ,注意这里再次出现了有序性。
- 内存中的Level 0树在达到阈值后,会在内存中遍历排好序的Level 0树并顺序写入磁盘的Level 1。同样的,在磁盘中的Level n(n>0)达到阈值时,则会将Level n层的多个文件进行归并,写入Level n+1层。(定义5) 除了内存中的Level 0层做原地更新外,对已写入磁盘上的数据,都采用Append形式的磁盘顺序写,即更新和删除操作并不去修改老数据,只是简单的追加新数据。图1中右侧蓝色的磁盘部分,Level 1和Level 2均包含key为2的数据,同时图1左侧绿色内存中的Level 0树也包含key为2的数据节点。(定义6)
下面我们遵循 LSM 树的 6 条定义,通过动图对 LSM 树的增、删、改、查和归并进行详细分析。
# 2. LSM 树的增删改查
# 2.1 插入操作
LSM树的插入较简单,数据无脑往内存中的Level 0排序树丢即可,并不关心该数据是否已经在内存或磁盘中存在。(已经存在该数据的话,则场景转换成更新操作)
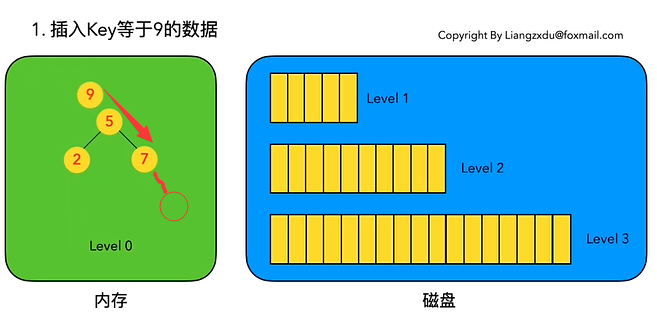
插入数据时,按照 key 的大小,插入内存中的 Level 0 排序树中,该操作复杂度为树高 log(n),n 为 Level 0 树的数据量,所以代价很低,能实现极高的写吞吐量。
# 2.2 删除操作
LSM树的删除操作并不是直接删除数据,而是通过一种叫“墓碑标记”的特殊数据来标识数据的删除。
删除操作分为:待删除数据在内存中、待删除数据在磁盘中 和 该数据根本不存在 三种情况。
# 2.2.1 待删除数据在内存中
将 Level 0 树中的对应节点采用墓碑标记将其覆盖。
示例:删除 key 等于 2 的数据,结果如下图所示:
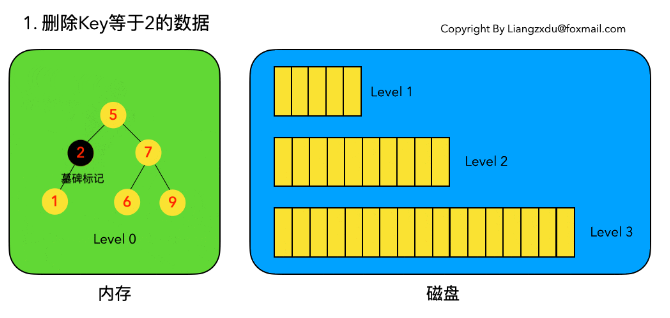
# 2.2.2 待删除数据在磁盘中
不去修改磁盘上的数据(理都不理它),而是直接向内存中的 Level 0 树中插入墓碑标记即可。
示例:删除 key 等于 2 的数据,结果如下图所示:
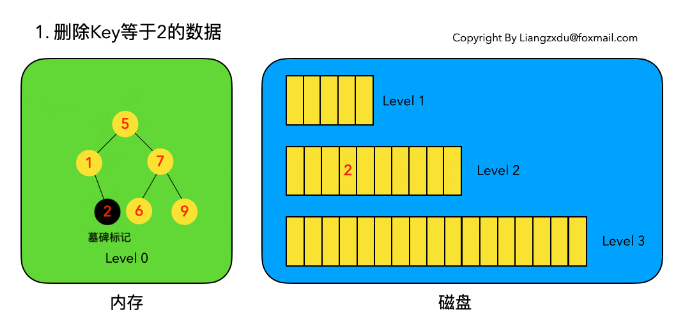
# 2.2.3 待删除数据不存在
这种情况等价于在内存的 Level 0 树中新增一条墓碑标记,场景转换为情况 2.2.3 的内存中插入墓碑标记操作。
综合看待上述三种情况,发现不论数据有没有、在哪里,删除操作都是等价于向 Level 0 树中写入墓碑标记。该操作复杂度为树高log(n),代价很低。
# 2.3 修改操作
LSM 树的修改操作和删除操作很像,也是分为三种情况:待修改数据在内存中、在磁盘中和 该数据根本不存在。
# 2.3.1 待修改数据在内存中
示例:修改 key=7 的数据。直接定位到内存中 Level 0 树上黄色的旧 key=7 的位置,将其覆盖。
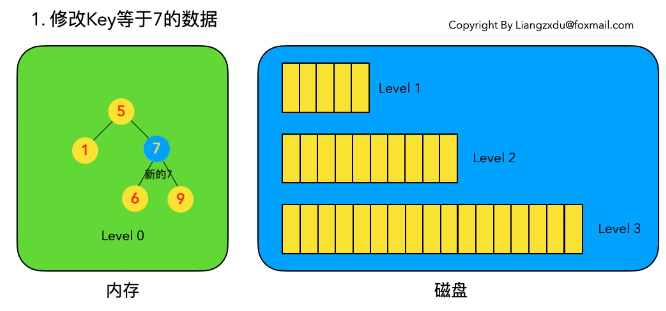
# 2.3.2 待修改数据在磁盘中
LSM 树并不会去磁盘中的 Level 1 树上原地更新老的 key=7 的数据,而是直接将新的蓝色的节点 7 插入内存中的 Level 0 树中。
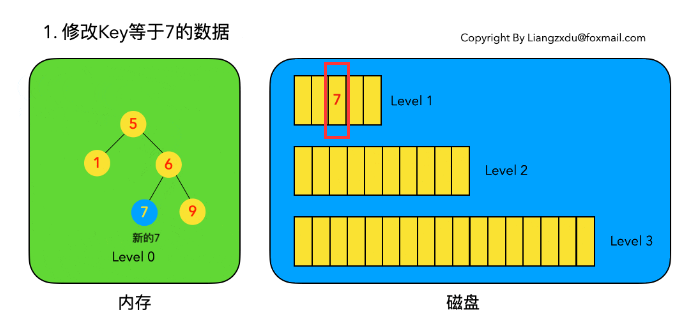
# 2.3.3 该数据不存在
此场景等价于情况b,直接向内存中的Level 0树插入新的数据即可。
综上三种情况可以看出,修改操作都是对内存中 Level 0 进行覆盖/新增操作。该操作复杂度为树高 log(n),代价很低。
我们会发现,LSM 树的增加、删除、修改(这三个都属于写操作)都是在内存中倒腾,完全没涉及到磁盘操作,所以速度飞快,写吞吐量高的离谱。。。
# 2.4 查询操作
LSM 树的查询操作会按顺序查找 Level 0、Level 1、Level 2 ... Level n 每一颗树,一旦匹配便返回目标数据,不再继续查询。该策略保证了查到的一定是目标 key 最新版本的数据(有点MVCC的感觉)。
我们来分场景分析:依然分为 待查询数据在内存中 和 待查询数据在磁盘中 两种情况。
# 2.4.1 待查询数据在内存中
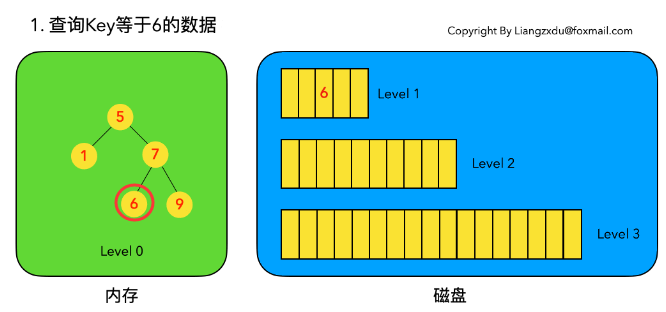
沿着内存中已排好序的Level 0树递归向下比较查询,返回目标节点即可。我们注意到磁盘上的Level 1树中同样包括一个key=6的较老的数据。但LSM树查询的时候会按照Level 0、1、2 ... n的顺序查询,一旦查到第一个就返回,因此磁盘上老的key=6的数据没人理它,更不会作为结果被返回。
# 2.4.2 待查询数据在磁盘中
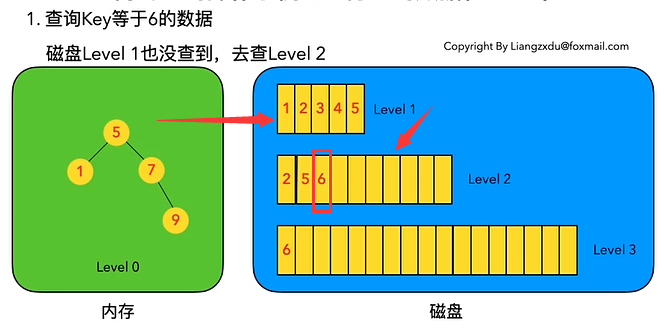
先查询内存中的Level 0树,没查到便查询磁盘中的Level 1树,还是没查到,于是查询磁盘中的Level 2树,匹配后返回key=6的数据。
综合上述两种情况,我们发现,LSM 树的查询操作相对来说代价比较高,需要从Level 0到Level n一直顺序查下去。极端情况是LSM树中不存在该数据,则需要把整个库从Level 0到Level n给扫了一遍,然后返回查无此人(可以通过 布隆过滤器 + 建立稀疏索引 来优化查询操作)。代价大于以B/B+树为基本数据结构的传统RDB存储引擎。
# 3. LSM 树的合并操作
合并操作是LSM树的核心(毕竟LSM树的名字就叫: 日志结构合并树,直接点名了合并这一操作)
之所以在增、删、改、查这四个基本操作之外还需要合并操作:
- 一是 内存 => 磁盘。因为内存不是无限大,Level 0树达到阈值时,需要将数据从内存刷到磁盘中;
- 二是 磁盘块1 + 磁盘块2 => 归并入下一层。需要对磁盘上达到阈值的顺序文件进行归并,并将归并结果写入下一层,归并过程中会清理重复的数据和被删除的数据(墓碑标记)。
我们分别对上述两个场景进行分析:
# 3.1 内存数据写入磁盘的场景
下图展示了内存中 Level 0 树在达到阈值后,归并写入磁盘 Level 1 树的场景。
归并之前:
归并之后:
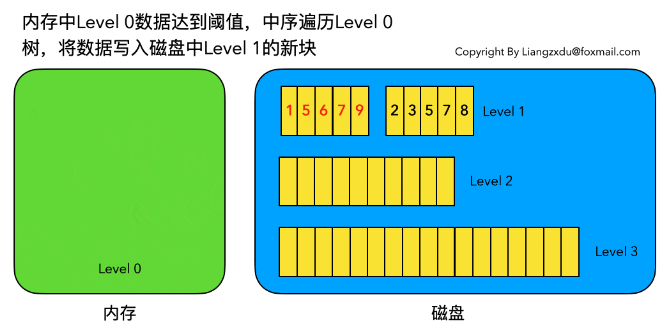
对内存中的Level 0树进行中序遍历,将数据顺序写入磁盘的Level 1层即可,我们可以看到因为Level 0树是已经排好序的,所以写入的Level 1中的新块也是有序的(有序性保证了查询和归并操作的高效)。
此时磁盘的Level 1层有两个Block块。
# 3.2 磁盘中多个块的归并
下图展示了磁盘中 Level 1 层达到阈值时,对其包含的两个 Block 块进行归并,并将归并结果写入 Level 2 层的过程。
归并之前:
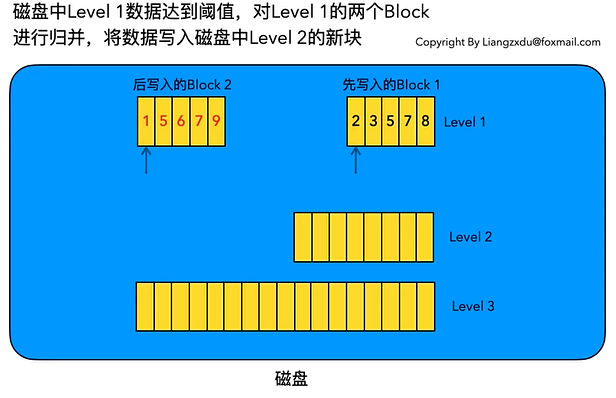
归并之后:
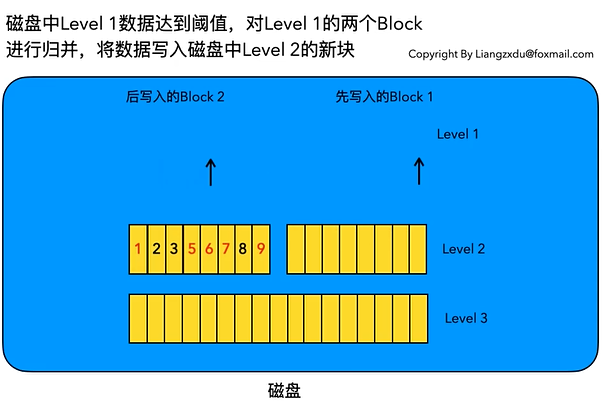
我们注意到 key=5 和 key=7 的数据同时存在于较老的Block 1和较新的Block 2中。而归并的过程是保留较新的数据,于是我们看到结果中,key=5和7的数据都是红色的(来自于较新的Block2)。
综上我们可以看到,不论是场景6.1还是场景6.2,由于原始数据都是有序的,因此归并的过程只需要对数据集进行一次扫描即可,复杂度为O(n)。
# 4. 优缺点分析
可以看到 LSM 树将增、删、改这三种操作都转化为内存 insert + 磁盘顺序写(当Level 0满的时候),通过这种方式得到了无与伦比的写吞吐量。
LSM 树的查询能力则相对被弱化,相比于 B+ 树的最多3~4次磁盘 IO,LSM 树则要从 Level 0 一路查询 Level n,极端情况下等于做了全表扫描。(即便做了稀疏索引,也是lg(N0)+lg(N1)+...+lg(Nn)的复杂度,大于B+树的lg(N0+N1+...+Nn)的时间复杂度)。
同时,LSM树只append追加不原地修改的特性引入了归并操作,归并操作涉及到大量的磁盘IO,比较消耗性能,需要合理设置触发该操作的参数。
综上我们可以给出LSM树的优缺点:
- 优:增、删、改操作飞快,写吞吐量极大。
- 缺:读操作性能相对被弱化;不擅长区间范围的读操作; 归并操作较耗费资源。
LSMTree的增、删、改、查四种基本操作的时间复杂度分析如下所示:
| 操作 | 平均代价 | 最坏情况代价 |
|---|---|---|
| 删除 | 1 | 1 |
| 插入 | 1 | 1 |
| 修改 | 1 | 1 |
| 查找 | lgN | lgN |
# 5. 总结
LSM树的设计原则:
- 先内存再磁盘
- 内存原地更新
- 磁盘追加更新
- 归并保留新值
如果说B/B+树的读写性能基本平衡的话,LSM树的设计原则通过舍弃部分读性能,换取了无与伦比的写性能。该数据结构适合用于写吞吐量远远大于读吞吐量的场景,得到了NoSQL届的喜爱和好评。
