 基本概念
基本概念
机器学习概括来说,机器学习就是让机器具备找一个函式的能力。
# Different types of Functions
Regression(回归)
输出是一个数值(scalar)
例如,今天要机器做的事情,是预测未来某一个时间的,PM2.5的数值。输入可能是种种跟预测PM2.5,有关的指数,这一个函式可以拿这些数值当作输入,输出明天中午的PM2.5的数值,那这一个找这个函式的任务,叫作Regression。
Classification(分类)
要机器做选择题。人类先备好一些选项(也叫类别)(classes),从设定好的选项中选择一个当做输出,这个任务就叫做 Classification。
例如,gmail account裡面有一个函式,帮我们侦测一封邮件,是不是垃圾邮件。
alpha go本身也是一个 Classification 的问题。
Structured Learning
- 机器今天不只是要做选择题,不只是输出一个数字,还要产生一个有结构的物件。机器画一张图 写一篇文章,这种叫机器产生有结构的东西的问题,就叫作Structured Learning。即要机器学会创造。
# Case Study
举例说明机器怎么找一个函式。
找一个函式,这个函式的输入是youtube上面一个频道过往所有的资讯,输出就是预测明天这个频道可能的总观看次数。
找这个函式的过程,分为三步:
- 写出一个带有未知参数的函式;2. 定义一个叫做Loss的function;3. 解一个Optimization的问题找到一组参数使loss值最小。<本质是训练,用已知的数据来“预测”>
# 1. Function with Unknown Parameters
假设函式为 $ y=b+w*x_{1} $,这个带有Unknown的Parameter的Function叫做Model。这个猜测往往就来自于你对这个问题本质上的了解,也就是 Domain knowledge
- y 为预测值,本例中为明天观看此频道的总人数
- $x_{1}$为已知的东西,叫做Feature,本例中为今天观看的人数
- b (bias) 和 w (weight)是未知的参数,要从数据资料中学习得到
# 2. Define Loss from Training Data
# (1) Loss 函数
定义一个 Loss 函数,输入为 Model 中的未知参数 b 和 w(Parameter),输出的值表示若把这组值传给未知参数,对于计算出的预测值是好还是不好。
对于 Loss 的计算,要从训练资料来进行。所以对于一个预测值,可以从训练资料中知道真实的结果,因而可以计算预估结果和真正结果(Label)之间的误差 e :$e_{i} = 计算差距(y,\hat{y} )$。可以以此方法计算训练集中的每一天的误差,从而可得 Loss 值:$L=\frac{1}{n}\sum_{n}e_{_n}$
L越大,代表这组参数越不好,L越小,代表这组参数越好
# (2) 计算误差e
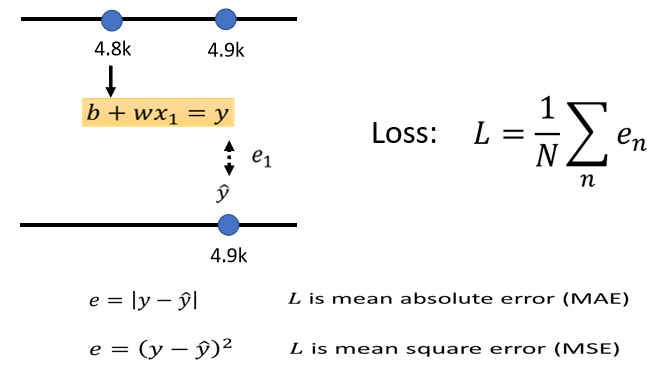
如上图,计算误差 e 有多种方法:MAE、MSN 、Cross-entropy(y 和 ŷ 机率分布时使用) 等。
# (3) Error Surface
我们可以调整不同的 w 和 b ,為不同的w跟b的组合计算它的Loss,然后就可以画出以下这一个等高线图.(尝试不同的参数,计算Loss,画出来的图)
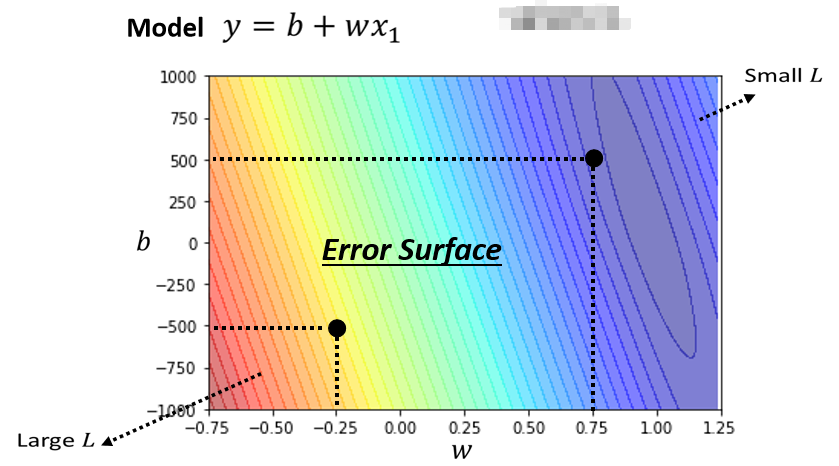
在这个等高线图上面,越偏红色系,代表计算出来的Loss越大,就代表这一组w跟b越差,如果越偏蓝色系,就代表Loss越小,就代表这一组w跟b越好。
# 3. Optimization
解一个最佳化的问题:找一组未知参数,让 Loss 最小。本例中是找让 Loss 最小的 w* 和 b*。一个Optimization 方法:Gradient Descent。
怎样找一个 w 让这个 loss 的值最小呢?随机选取一个初始的点,这个初始的点,我们叫做 w0-> 求参数对 Loss 的微分 -> 更新参数值。朝低的地方跨一步,那更新时这一步要跨多大呢?这一步的步伐的大小取决于这个地方的斜率和学习率 ($\eta $)(自己设定的)。这种你在做机器学习,需要自己设定的东西,叫做hyperparameters (超参数)。
什么时候停下来呢?往往有两种状况:
- 第一种状况是你失去耐心了,你一开始会设定说,我今天在调整我的参数的时候,我最多计算几次;
- 那还有另外一种理想上停下来的可能是,今天当我们不断调整参数时调整到一个地方,它的微分的值算出来正好是 0 的时候,如果这一项正好算出来是0.0乘上 learning rate 还是 0,所以你的参数就不会再移动位置,那参数的位置就不会再更新。
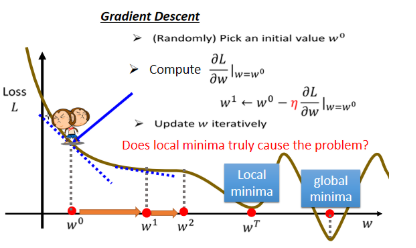
你可能会发现 Gradient Descent 这个方法有一个巨大的问题,我们没有找到真正最好的解,我们只是找到的 local minima 而不是 global minima。其实,local minima 是一个假问题,我们在做 Gradient Descent 的时候真正面对的难题不是 local minima,之后会讲到它的真正痛点在哪。
刚刚只有一个参数 w,将其扩展至二维乃至多维是同理。

optimization
# Linear Model
上文中的模型即线性模型。
观察真实数据,发现每隔七天一个循环,因此可以修改模型(模型的修改通常来自于对问题的理解,即 Domain Knowledge)。因而模型从$y=b+wx_1$ --> $y=b+ \sum_{j=1}^{7}w_jx_j$,前七天的观看人数都被列入考虑。
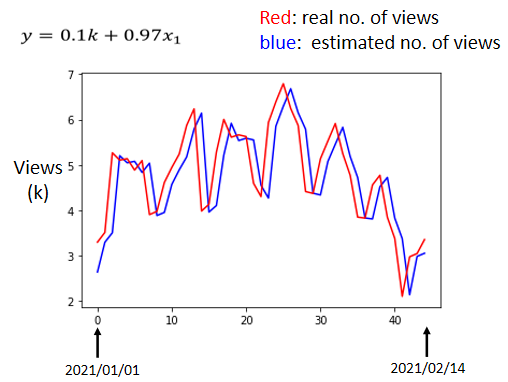
# Piecewise Linear Curves(分段线性曲线)
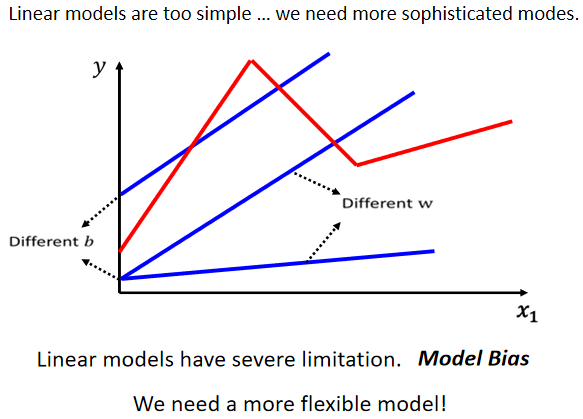
不管怎麼摆弄w 跟 b,你永远製造不出红色那一条线,你永远无法用 Linear 的 Model,製造红色这一条线。因为 model 的限制而使得永远无法模拟真实状况,这种来自 Model 的限制,叫做Model 的 Bias(≠上文中 Model 中的 Bias b)。
# 1. 红色曲线怎么表达
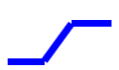
图中红色的这一条曲线,可以看作是一个常数,加上一群蓝色这样的 Function。
这个蓝色的 Function 叫做 Hard Sigmoid,它的特性是
- 当输入的值,当 x 轴的值小於某一个这个 Flash Hold 的时候,它是某一个定值,
- 大於另外一个 Flash Hold 的时候,又是另外一个定值,
- 中间有一个斜坡
Piecewise Linear 的 Curves 越复杂,也就是这个转折的点越多啊,那你需要的这个蓝色的 Function 就越多。可以用 Piecewise Linear 的 Curves,去逼近任何的连续的曲线,而每一个 Piecewise Linear 的 Curves,又都可以用一大堆蓝色的 Function 组合起来,也就是说,我只要有足够的蓝色 Function 把它加起来,我也许就可以变成任何连续的曲线。
# 2. 蓝色 Function (Hard Sigmoid)怎么写出来
# (1)Sigmoid Function(S型曲线)
用 sigmoid Function 来逼近蓝色 Function。公式:
$y=c\frac{1}{1+e^{b+wx_1}} =c*sigmoid(b+wx_1) $
# (2) 各式各样的蓝色 Function 怎样制造出来
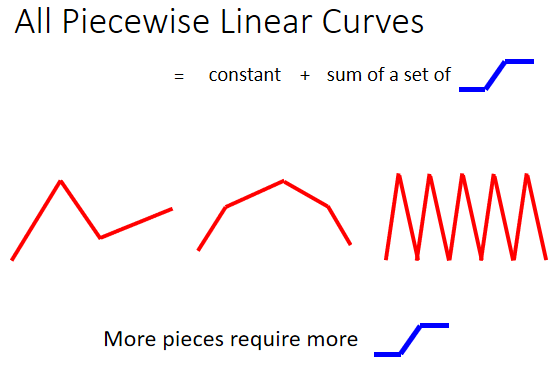
调整 b 、w 和 c :
如果你今天改 w 你就会改变斜率你就会改变斜坡的坡度
如果你动了 b 你就可以把这一个 Sigmoid Function 左右移动
如果你改 c 你就可以改变它的高度
不同的 Sigmoid Function 叠起来以后,可以去逼近各种Piecewise Linear 的 Function,然后可以用来来近似不同的连续函数。
# 3. 红色 Function 长什么样子
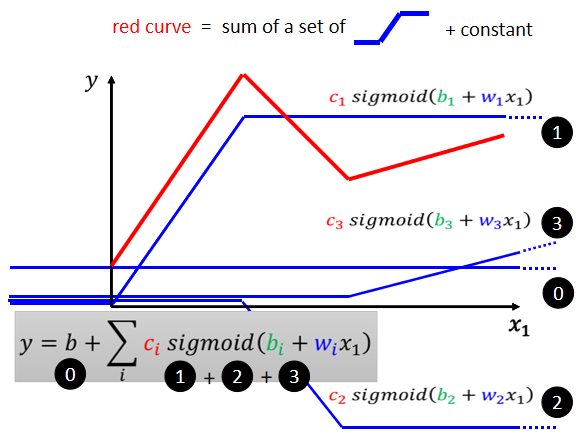
红色曲线 = 蓝色0+1+2+3,即
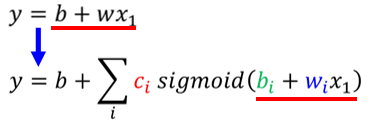
# 如何减少 Model 的Bias
写一个更有弹性的,有未知参数的 Function:

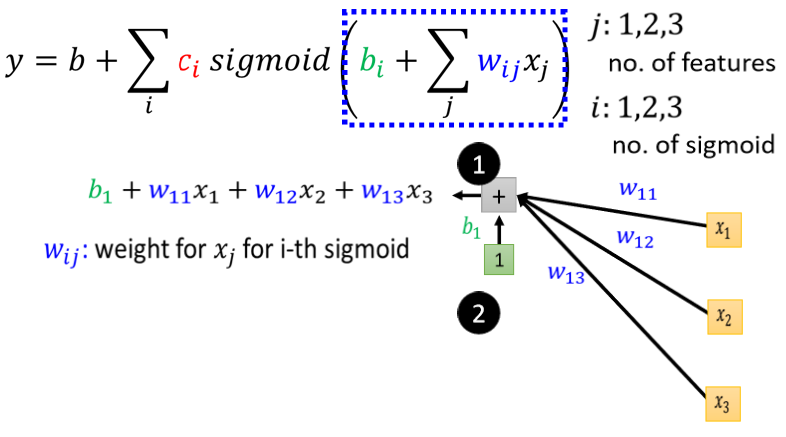
此时,用了多个Feature,即$X_1$。 j 来代表 Feature 的编号.
我们先考虑一下 j 就是 1 2 3 的状况,就是我们只考虑三个 Feature。举例来说 我们只考虑前一、二、三天的 Case,
所以 j 等於 1 2 3,那所以输入就是 x1 代表前一天的观看人数,x2 两天前观看人数,x3 三天前的观看人数
每一个 i 就代表了一个蓝色的 Function,只是我们现在每一个蓝色的 Function,都用一个 Sigmoid Function 来比近似它,1 2 3 代表有三个 Sigmoid Function,
这个括号裡面做的事情是什麼:
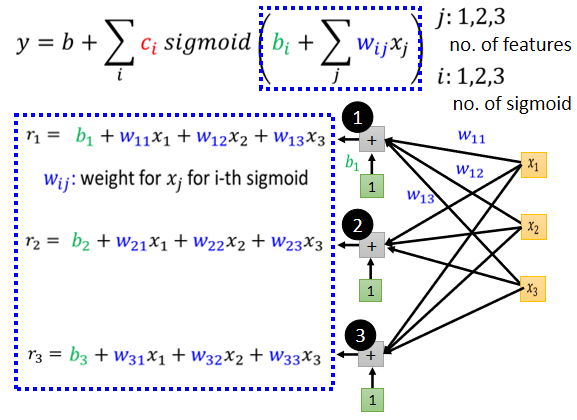
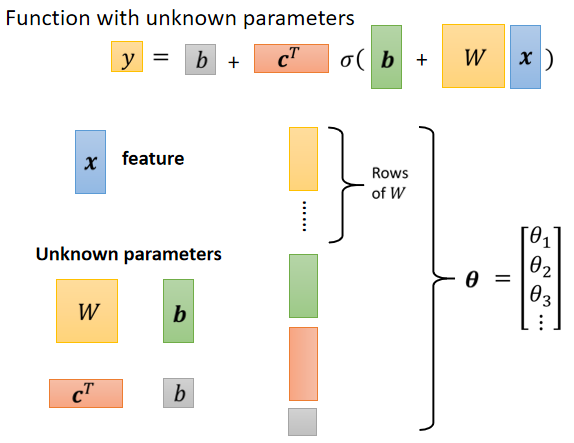
表达成矩阵形式:

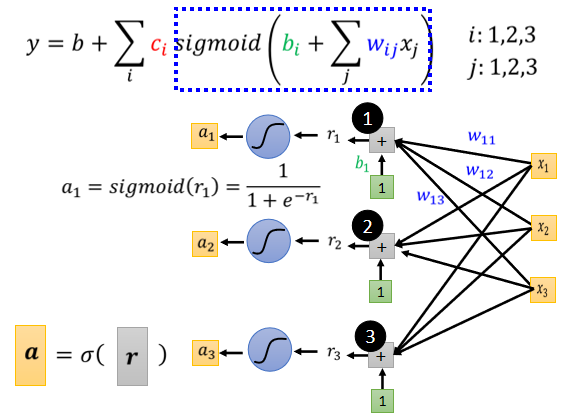 这个蓝色方框做的事情:
这个蓝色方框做的事情: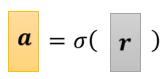
接下来:
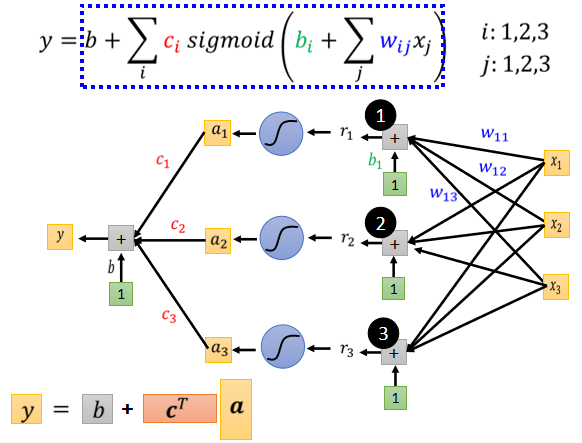
整个过程做的事情为: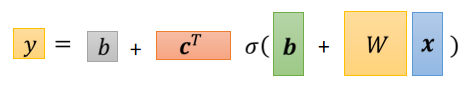
**重新定义符号:**各个列向量拼在一起,统称为$\theta$.
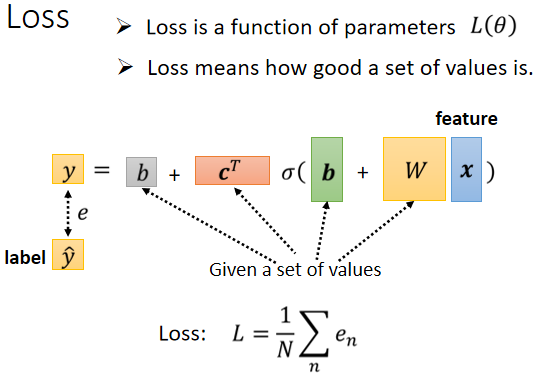
# Back to ML_Step 2 :define loss from training data
直接用 θ 来统设所有的参数,所以我们现在的 Loss Function 就变成 $L(\theta)$.
# Back to ML_Step 3: Optimization

一直按照这个图计算下去,直到 Gradient=0 向量的结果或者不想做了。
但是实际上,我们的数据集通常会很大,假设为 N ,我们把这 N 笔资料分成一个个组,一组叫 Batch,并且只拿一个 Batch 里的 Data 算一个 Loss,把他叫做 L1。假设这个 B 够大,也许 L 跟 L1 会很接近 也说不定,所以实作上的时候,每次我们会先选一个 Batch,用这个 Batch 来算 L,根据这个 L1 来算 Gradient,用这个 Gradient 来更新参数,接下来再选下一个 Batch 算出 L2,根据 L2 算出 Gradient,然后再更新参数,再取下一个 Batch 算出 L3,根据 L3 算出 Gradient,再用 L3 算出来的 Gradient 来更新参数,如下图: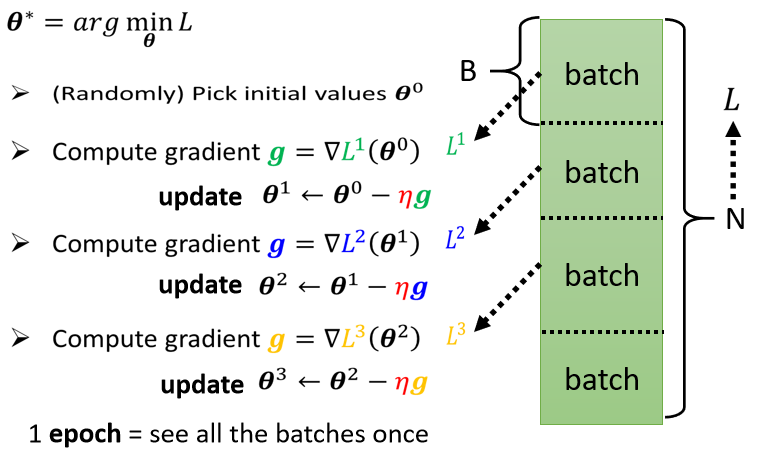 所以我们并不是拿 L 来算 Gradient,实际上我们是拿一个 Batch 算出来的 L1 L2 L3,来计算 Gradient,那把所有的 Batch 都看过一次,叫做一个 Epoch,每一次更新参数叫做一次 Update,Update 跟 Epoch 是不一样的东西。Batch Size 也是一个 HyperParameter。
每次更新一次参数叫做一次 Update,把所有的 Batch 都过一遍,叫做一个 Epoch。
所以我们并不是拿 L 来算 Gradient,实际上我们是拿一个 Batch 算出来的 L1 L2 L3,来计算 Gradient,那把所有的 Batch 都看过一次,叫做一个 Epoch,每一次更新参数叫做一次 Update,Update 跟 Epoch 是不一样的东西。Batch Size 也是一个 HyperParameter。
每次更新一次参数叫做一次 Update,把所有的 Batch 都过一遍,叫做一个 Epoch。
# 模型变型
# Activation Function
- Sigmoid(S型)
- ReLU(Rectified Linear Unit)
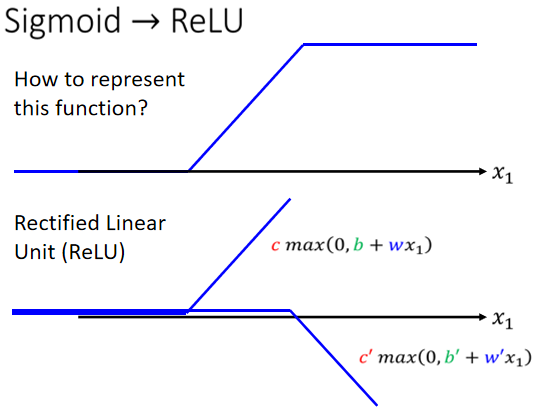
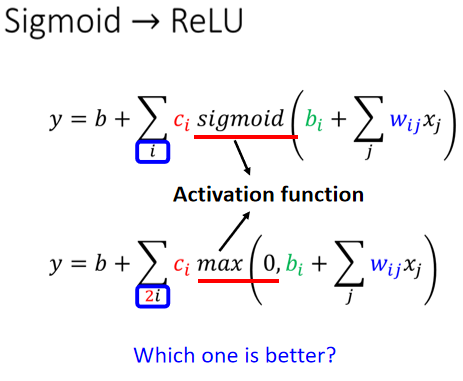
把两个 ReLU 叠起来,就可以变成 Hard 的 Sigmoid,你想要用 ReLU 的话,就把 Sigmoid 的地方,换成$max(0, b_i+w_{ij}x_j)$.
接下来的实验都选择用了 ReLU,显然 ReLU 比较好.原因下回分解
# 模型改进——多做几次
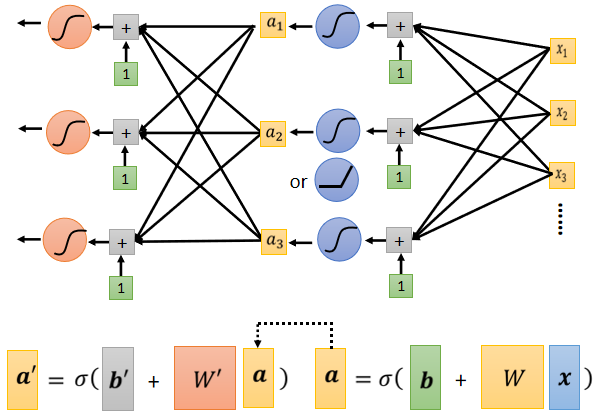
Deep Learning:Neural Network换个了名字,重振雄风。如下图:
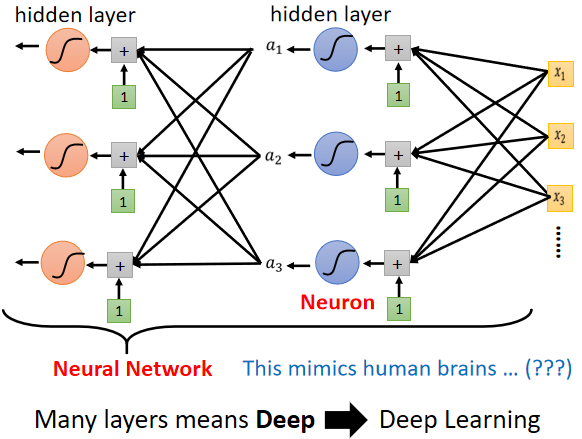
Over Fitting:更深层次之后,在训练集上效果更好,但是预测的效果更差了。
